remarque : le cours sera fait d’activités d’applications – le cours sera sur fiche –
Définition de la proportionnalité : deux grandeurs sont proportionnelles si elles varient dans les mêmes proportions, c’est à dire que si l’une de deux double, alors l’autre double aussi (si l’une est x3, alors l’autre est multipliée par 3, si l’une est divisée par 4, alors l’autre est divisée par 4, …).
En sciences, beaucoup de grandeurs sont proportionnelles entre elles : Reconnaître une situation de proportionnalité permet de prévoir les valeurs d’une grandeur quand on connaît les autres grandeurs.
Comment identifier une situation de proportionnalité ?
1ère méthode : dans un tableau de valeur
On cherche le rapport entre les deux grandeurs = on divise les valeurs de la grandeur 1 et de la grandeur 2 : les grandeurs sont proportionnelles si on trouve toujours le même nombre (= constante), appelé le
coefficient de proportionnalité.
.
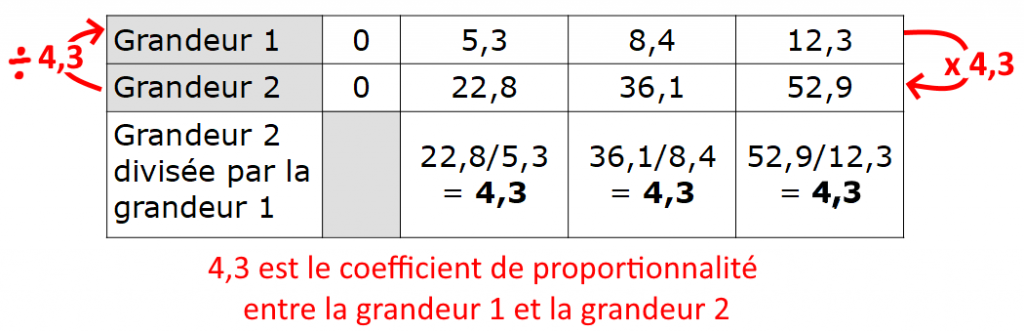
Remarque : en sciences expérimentales, le rapport est rarement parfaitement égal à cause de l’imprécision des mesures et des erreurs expérimentales.
2ème méthode : avec un graphique
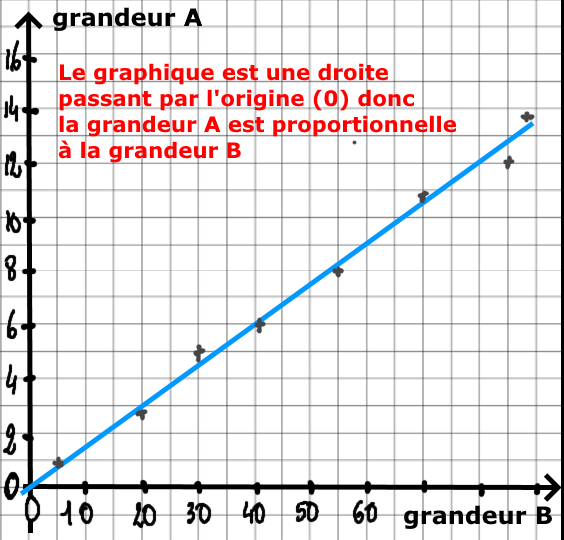
On regarde l’allure du graphique de la grandeur A en fonction de la grandeur B.
Si deux grandeurs sont proportionnelles, alors le graphique est une droite passant par l’origine.
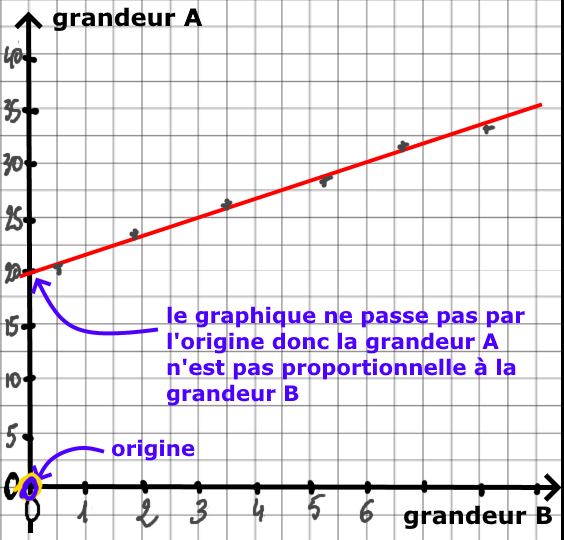
Si le graphique n’est pas une droite passant par l’origine, alors les deux grandeurs ne sont pas proportionnelles.
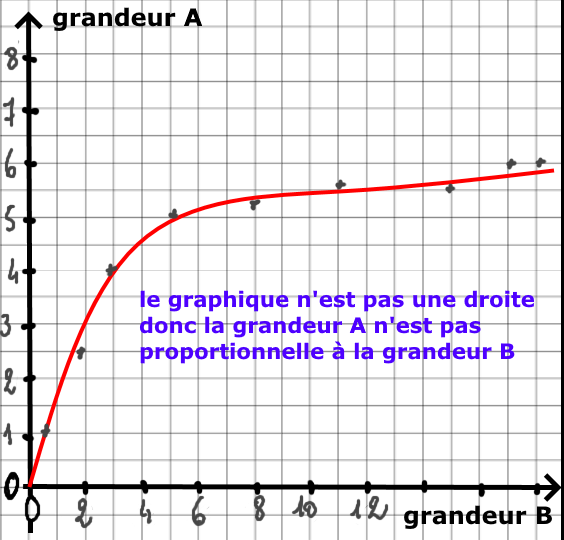
3ème méthode : avec un relation mathématique
Si deux grandeurs sont proportionnelles, alors il existe une relation mathématique les reliant, du type :
grandeur A = coefficient de proportionnalité x grandeur B
En sciences expérimentales, on donne souvent un nom particulier au coefficient de proportionnalité.
loi d’ohm : Coefficient de proportionnalité = R = résistance.
Relation du poids : coefficient de proportionnalité = g = intensité de pesanteur
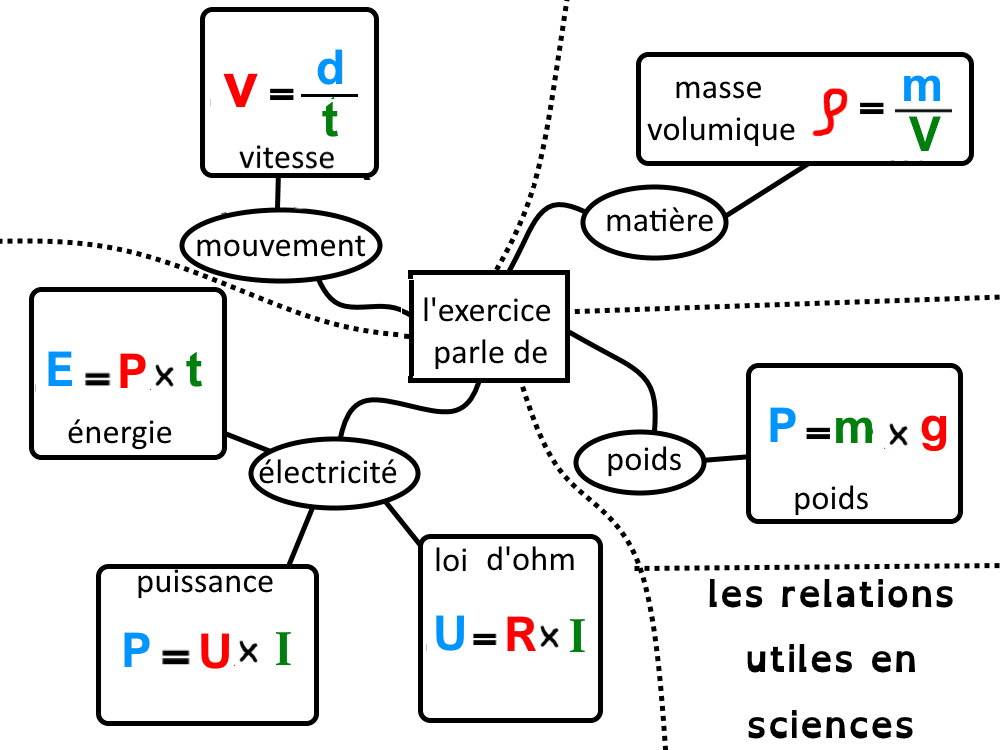
Remarques : si la relation contient une addition ou un soustraction, il n’y a pas de relation de proportionnalité.
