corrigé – activité 2 p257 du manuel
J’exploite les documents scientifiques :
Citez vos sources dans les réponses. Si on exploite des documents, la plupart des réponses sont dans le document donc lisez le document…
1) Lors d’une chute, l’objet descend donc l’altitude diminue.
D’après le document 3, la vitesse augmente puisqu’elle passe de 0 km/h (départ) à 3,6 km/h (vitesse maximale juste avant l’atterrissage)
2) D’après le document 1, plus l’altitude est grande, plus l’énergie potentielle est grande donc comme l’altitude diminue au cours de la chute de Philae, on en déduis que l’énergie potentielle diminue.
D’après le document 2, l’énergie dépend de la masse et de la vitesse de l’objet donc comme la vitesse augmente, l’énergie cinétique augmente.
3) D’après mes réponses à la question 2, je vois que l’énergie potentielle diminue alors que l’énergie cinétique augmente. Dans les graphiques présentés, la barre bleue diminue alors que la barre rouge augmente. J’en déduis que la barre bleue représente l’énergie potentielle et que la barre rouge représente l’énergie cinétique. La barre verte représente forcément la somme de ces deux énergies.
Note : la somme des deux énergies s’appelle l’énergie mécanique (ce point est noté dans le blog mais pas sur le manuel, c’est cependant utile de le savoir).
Je calcule :
Rédiger en écrivant la formule littérale, en citant la source qui vous donne la masse et la vitesse, en écrivant le calcul et le résultat AVEC LA BONNE UNITÉ (énergie → joule)
4) Pour calculer l’énergie cinétique de Philae lorsque le robot a atteint sa vitesse maximale, j’utilise la relation :
Ec = 1/2 mv2 avec m = 100 kg et v = 3,6 km/h d’après le document 3
Il faut convertir la vitesse en m/s : v = 3,6/3,6 = 1 m/s
donc Ec = 1,2 x 100 x 1
Ec = 50 J
L’énergie cinétique de Philae vaut 50 J.
J’interprète des résultats :
« Estimer » veut dire « donner une valeur sans calcul » donc pas besoin d’aller chercher la relation qui permet de calculer l’énergie potentielle (mais bravo à ceux qui ont fait des recherches pour cela…si vous avez compris ce que vous avez fait!)
Là encore, dans une étude documentaire, vous devez vous servir de ce que l’on vous donne dans le document (avec en plus vos connaissances personnelles comme « savoir comment convertir une vitesse en m/s »…)
5) D’après la question 3) et le document 2) on sait que l’énergie potentielle se convertit en énergie cinétique lors de la chute mais que le total des 2 énergies reste le même.
A la fin de la chute, toute l’énergie potentielle s’est convertie en énergie cinétique et celle-ci vaut 50 joules. Cela veut dire qu’au départ, l’énergie potentielle avait une valeur équivalent, soit 50 joules.
je communique avec un langage scientifique :
En conclusion : On peut écrire que lors d’une chute, l’énergie potentielle diminue et l’énergie cinétique augment car l’énergie potentielle se convertie en énergie cinétique. Si on néglige les frottements, la somme des deux énergies se conserve.
Note : s’il y a des frottements (ce qui arrive lorsqu’il y a une atmosphère), une partie de l’énergie potentielle se convertie en énergie thermique (cette énergie thermique est très importante lors d’une chute de poussières de météorites : celles-ci s’enflamment dans l’atmosphère à cause de cette énergie thermique et forment les étoiles filantes).
Il faut aussi mettre des matériaux résistants à la chaleur pour les navettes spatiales pour la même raison. Dans ces cas-là, les frottements ne sont pas négligeables.
Sur la comète Tchouri, comme il n’y a pas d’atmosphère, les frottements sont négligeables.
Pour aller plus loin – sécurité routière et conversion d’énergie :
Cette partie était plus difficile si on veut la faire de manière complète.
Rappel : on admet que l’énergie de position se transforme entièrement en énergie cinétique (pas de frottement) donc on peut écrire que l’énergie de position du départ est égale à l’énergie cinétique à la fin soit Ep = Ec.
On rappelle que Ec = 1/2 m v2
et que Ep est proportionnelle à la masse et à la hauteur soit Ep = 10 x m h avec m la masse en kilogramme, h la hauteur en mètre et 10 le coefficient de proportionnalité.
1) L’énergie de position (ou potentielle) se transforme entièrement en énergie cinétique donc l’énergie potentiel du départ est égale à l’énergie cinétique à la fin de la chute
on peut écrire : Epdébut = Ecfin
or Epdébut = 10 x m h et Ecfin = 1/2 m v2
On peut trouver la solution sans « passer » par des calculs avec des chiffres…Mais il faut être à l’aise avec les équations…

Cette méthode permet de prouver que cette égalité est vraie quelque soit la masse de l’objet.
On peut aussi noter que, comme la masse n’apparait pas dans la relation finale, deux objets qui tombent de la même hauteur iront à la même vitesse, qu’ils soient lourd ou légers (si on néglige les frottements de l’air!)
Mais on peut aussi choisir de manière arbitraire une masse et faire les calculs pour vérifier l’égalité.
Cette manière n’est pas très scientifique (mais acceptable au collège) car il faudrait vérifier pour TOUTES les masses…Ce qui n’est pas faisable.
Par le calcul : je choisis une masse de 1000 kg (réaliste pour une voiture mais pas non plus trop compliqué pour le calcul. Restons simple!)
Ec = 1/2 x m xv2 avec m = 1000 kg et v = 50 km/h = 13,9 m/s
Ec = 0,5 x 1000 x 13,92 = 96 605 J
Ec = Ep donc Ep = 96 605 J
Ep =10 x m x h donc 96 605 = 10 x 1000 x h donc h = 96 605/10000 = 9,66 m
or v2 / 20 = 13,92 /20 = 193,21/20 = 9,66
on a bien h = v2 / 20
2) On peut ensuite vérifier les données de l’image pour chaque vitesse :
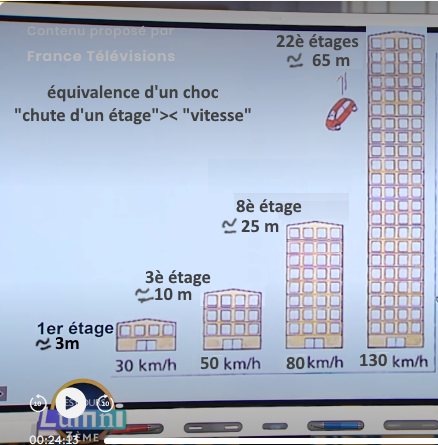
Pour v= 30 km/h = 8,3 m/s, on a h = 8,32/ 20 = 3,4 m ce qui correspond à peu près au 1er étage (3 m)
Pour v = 50 km/h= 13,9 m/s, on a h = 9,66 m ce qui correspond à peu près au 3eme étage (10 m)
Pour v = 80 km/h= 22,2 m/s, on a h = 22,22/ 20 = 24,6 m ce qui correspond à peu près au 8eme étage (25 m)
Pour v = 130 km/h= 36,1 m/s, on a h = 36,12/ 20 =65,1 m ce qui correspond à peu près au 22eme étage (65 m)
Les données de l’image sont correctes




