Activité 1
Étude des variations de l’énergie cinétique en fonction de la masse.
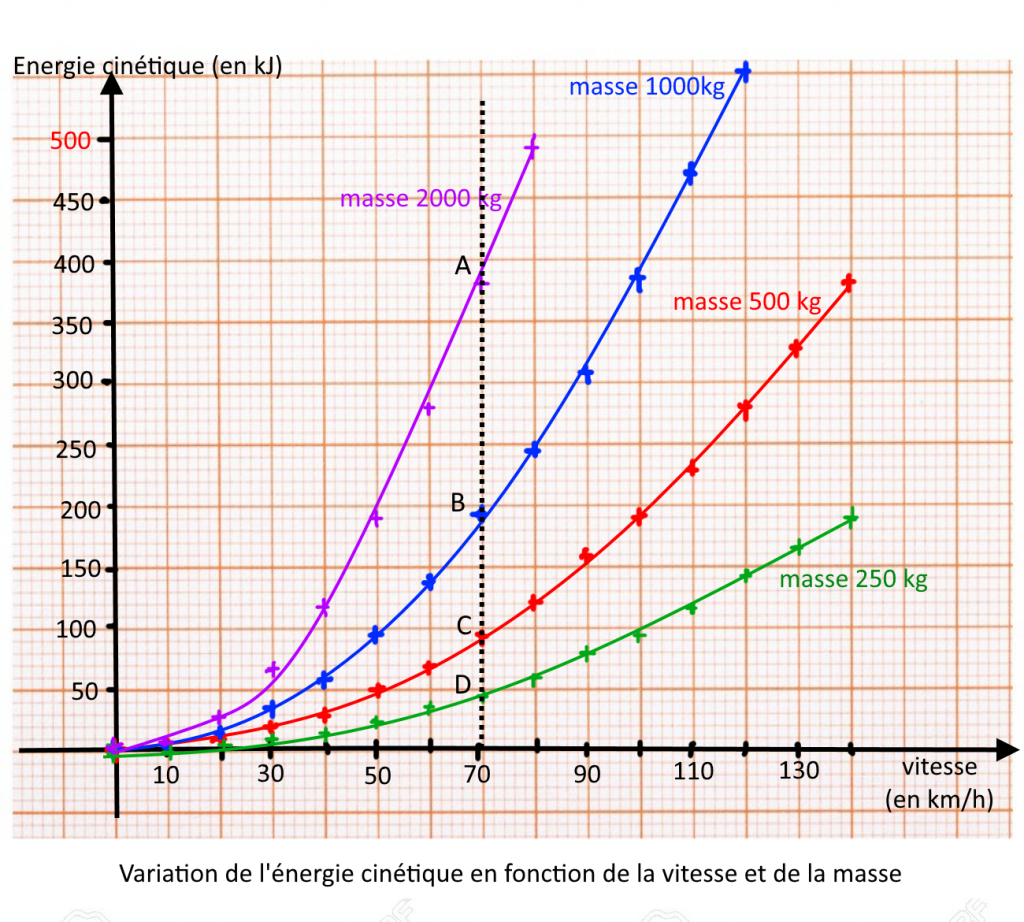
1) D’après le graphique (flèche noire sur ligne pointillée), la valeur de l’énergie cinétique à 70 km/h est de :
- 45 kJ pour une masse de 250 kg (courbe verte)
- 95 kJ pour une masse de 500 kg (courbe rouge)
- 190 kJ pour une masse de 1000 kg (courbe bleue)
- 380 kJ pour une masse de 2000 kg (courbe violette)
2) Pour savoir si l’énergie cinétique est proportionnelle à la masse, il faut vérifier qu’il existe un coefficient de proportionnalité :
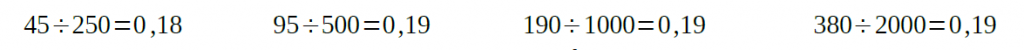
On observe que le coefficient est presque le même, donc, si on prend en compte les erreurs de précision, on peut conclure que l’énergie cinétique est bien proportionnelle à la masse.
Il est possible de faire le calcul inverse (masse divisée par énergie), dans ce cas, on trouve un coefficient d’environ 5,2
3) plus la masse d’un objet est grande, plus l’énergie cinétique est grande.
Étude des variations de l’énergie cinétique en fonction de la vitesse.
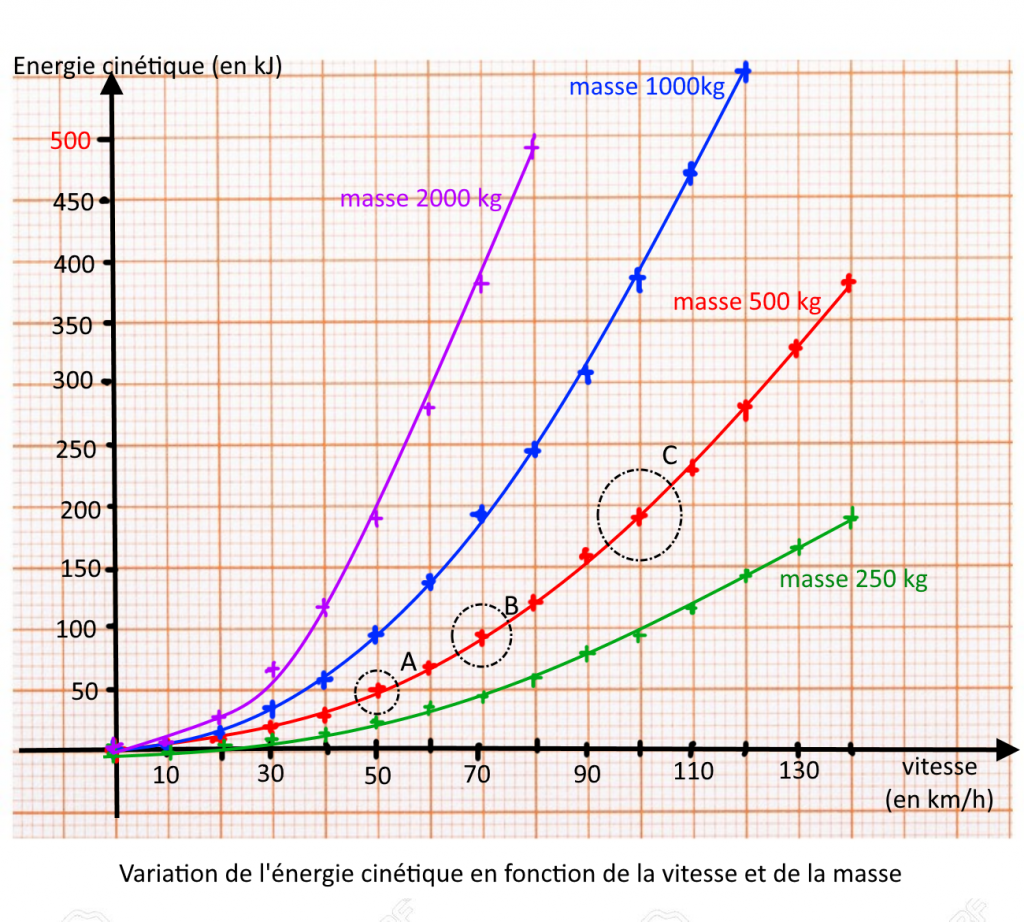
4) D’après le graphique (cercles sur courbe rouge), la valeur de l’énergie cinétique pour une masse de 500 kg est de :
- 50 kJ à une vitesse de 50 km/h
- 95 kJ à une vitesse de 70 km/h
- 190 kJ à une vitesse de 100 km/h
5) le graphique de l’énergie en fonction de la vitesse n’est pas une droite passant par zéro donc l’énergie cinétique n’est pas proportionnelle à la vitesse.
On peut trouver ce résultat encore autrement en comparant deux résultats :
Si on double la vitesse (on passe de 50 km/h à 100 km/h), on constate que l’énergie ne double pas mais augmente de manière plus importante : le double de 50 kJ est 100 kJ alors que l’énergie cinétique à 100 km/h est de 190 kJ. On en déduit que les deux grandeurs ne sont pas proportionnelles.
On peut aussi utiliser la même méthode que précédemment en vérifiant s’il existe un coefficient de proportionnalité. On constate que les résultats changent et qu’il n’existe donc pas de coefficient de proportionnalité.
6) Plus la vitesse d’un objet est grande, plus l’énergie cinétique est grande. (même si elle n’est pas proportionnelle à la vitesse)
Conclusion : l’énergie cinétique d’un objet dépend de sa masse et de sa vitesse
Activité 2 : comment calculer l’énergie cinétique d’un objet ?
Les erreurs principales ont été : vous n’avez pas converti la vitesse en mètre par seconde et vous avez oublié le carré de la vitesse.
Ah! et d’autres ont mis des énergies en km/h, en m/s, en kg, en h bref dans toutes sortes d’unités qui n’ont rien à voir avec l’énergie!
1) à la vitesse de 30 km/h, l’énergie cinétique vaut :
Ec = 1/2 mv2 avec m = 500 kg et v = 30 km/h = 30/3,6 ≈ 8,3 m/s
Ec = 0,5 x 500 x 8,32 = 0,5 x 500 x 8, 3 x 8,3 ≈ 17 222 J
(si vous n’arrondissait pas la vitesse à 8,3 m/s, vous pouvez trouver un résultat entre 17 347 à 17 361 J)
2) à la vitesse de 60 km/h (le double de 30 km/h), l’énergie cinétique vaut :
Ec = 1/2 mv2 avec m = 500 kg et v = 60 km/h = 60/3,6 ≈ 16,7 m/s
Ec = 0,5 x 500 x 16,72 = 0,5 x 500 x 16,7 x 16,7 ≈ 69722 J
(si vous n’arrondissait pas la vitesse à 16,7 m/s, vous pouvez trouver un résultat entre 69 444 à 69 722 J)
3) Lorsque la vitesse double, l’énergie cinétique est multipliée par 4
(il faut faire le calcul : 69722 J divisé par 17 222 J)
4) à la vitesse de 90 km/h (le triple de 30 km/h), l’énergie cinétique vaut :
Ec = 1/2 mv2 avec m = 500 kg et v = 90 km/h = 90/3,6 = 25 m/s
Ec = 0,5 x 500 x 252 = 0,5 x 500 x 25 x 125 = 156 250 J
5) Lorsque la vitesse triple, l’énergie cinétique est multipliée par 9
(il faut faire le calcul : 156 250 J divisé par 17 222 J)
6) Lors d’un accident, l’énergie cinétique se transforme en énergie de déformation or plus la vitesse est grande, plus l’énergie cinétique est grande et donc plus l’énergie de déformation sera grande lors du choc. De plus, on voit que lorsque la vitesse double, l’énergie cinétique est multipliée par 4 donc l’énergie de déformation sera aussi multipliée par 4 : on peut dire que les dégâts peuvent être 4 fois plus importants alors que la vitesse n’a que doublé.
Voilà pourquoi on peut dire que les dégâts augmentent de manière très importante avec la vitesse lors d’un accident.




